Introduction
One of central beliefs in an ideal free market system is that the single-minded pursuit of self-interest will also promote group interest. But in the real market, the costs and benefits of each option depend upon the choices of other individuals. Blind pursuit of self-interest may result in sub-optimal individual and group outcome. Behavior to navigate such game-theoretic situations is called strategic.
The Invisible Hand Game
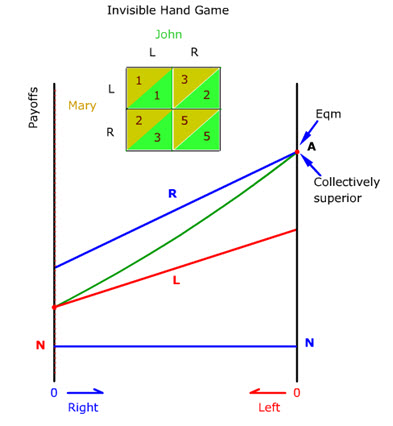
Strategic situations are commonly represented by a 2 by 2 payoff matrix. In the invisible-hand situation where self-interests and group interests are compatible, the matrix might look like this. There are two individuals, John and Mary and two options, the right choice, R and the left choice, L. The payoffs of Johnís choices are colored green and the payoffs of Maryís choices are colored tan. The numbers are cardinal index of possible payoffs. There are four possible combinations of choices. Mary's left choice could be combined with John's left choice, or John's right choice. Or Mary's right choice could be combined with John's left choice, or John's right choice.
In this situation, the optimal choice pair is RJohn and RMary with each scoring 5 (circle). John and Mary can always end up in this choice pair as long as they head for R. And each can depend on the other to do so because the payoff for choosing R always trumps the payoff for choosing L. For Mary, the payoff for R (circle) is always greater than for L (circle). And for John, the payoff for R (circle) is always greater than for L (circle). In other words, R is the dominant strategy. And RJohn and RMary is a stable solution (circle) from which nobody has any incentive to defect. It is technically known as a Nash equilibrium.
This payoff matrix is difficult to grasp quickly and its two-person limit unnecessarily confining.
Letís graph the payoff matrix by extending it into N number of people (animate). The payoff for choosing R goes linearly from left to right starting at 2 and ends up at 5 as the number of people choosing R increases from left to right (animate). The payoff for choosing L goes linearly from right to left starting at 3 and ends up at 1 as the number of people choosing L increases from right to left (animate). The end points of the payoff curves correspond to the 2 by 2 payoff matrix. A quick glance at this graph shows that R dominates L because the payoff for R is entirely above the payoff for L. Since each person choosing the same option has identical payoff, the collective payoff at each point along the horizontal axis is the weighted average of the payoff for each option at that point. The weights are the percentages of people choosing each option (animate).
The highest collective payoff occurs when everybody chooses R at A. At this point, nobody has any incentive to choose L. So A is both a collectively superior and a stable equilibrium solution (animate).
In this invisible-hand game, R represents the single-minded pursuit of self-interests. L is the abstinence from such pursuit.
Because there is no conflict between individual payoff and group payoff, the invisible-hand situation is strictly speaking not strategic. But it is a good benchmark to compare with typically strategic situations.
The PD Game
In Adam Smith's invisible-hand game, self-interest and group interest are compatible because the option R that delivers increasing payoffs with more supporters (animate) dominates the option L that delivers decreasing payoffs with more supporters (animate). As a result, the collectively superior solution at A where everybody chooses R as indicated by the green collective payoff curve is also stable (animate).
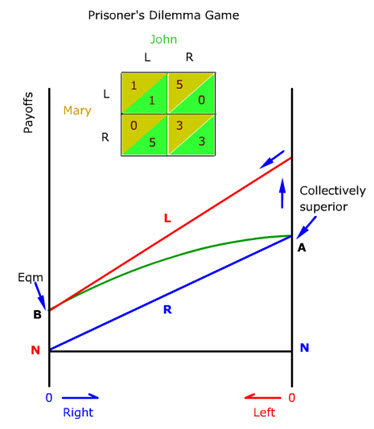
But if the dominance between the R and L options is reversed, the option L that delivers decreasing payoffs with more supporters will dominate option R that delivers increasing payoffs with more supporters. The invisible-hand game then becomes the classic prisoner's dilemma game where self-interest conflicts with group interest (circle title).
The game is so named because the original story involved two suspects in a joint crime who are struggling over whether each should confess separately to get a lighter sentence or remain collectively silent to escape any punishment.
Although the collectively superior solution still occurs at A where everybody chooses R as indicated by the green collective payoff curve, A is no longer a stable solution (animate).
The higher payoffs from option L offer constant temptation to defect from R (one upward arrow). This defection will continue until everybody chooses L at B, a stable but collectively inferior solution (animate).
The situation of cheating comes to mind. People are collectively better off when most donít cheat. But the few individuals who cheat are even better off if they can get away with cheating. People are collectively worse off when most routinely cheat. But there is no self-correcting mechanism to get out of an entrenched cheating culture.
The PD II Game
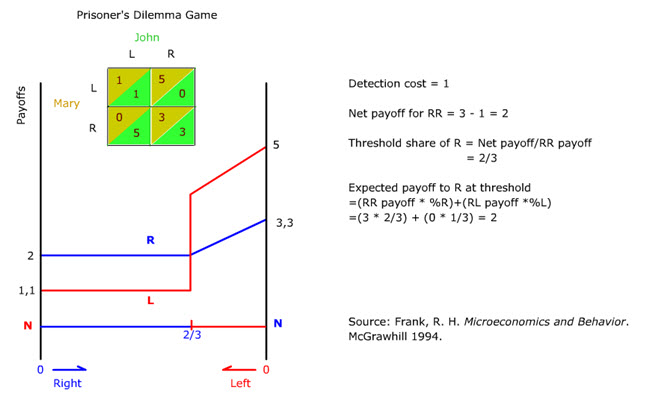
But the R choosers are not powerless to prevent wholesale defection to L. L's payoffs are higher than R's payoffs only if the identity of L choosers is not known. If L choosers can be excluded by incurring a detection cost of 1 unit (animate), then the R chooser's net payoff would never fall below 2 (animate). And L chooser's payoff would never rise above 1 since L choosers will be dealing only among themselves (animate).
Some L choosers would remain because R choosers would not incur the detection cost unless the percentage of L exceeds 1/3. When the percentage of L choosers is 1/3, the expected payoff to R without detection would be just equal to the payoff to R with detection (animate).
So defection from R will be stopped once the acceptable threshold share of L choosers is reached (animate).
The Coordination Game
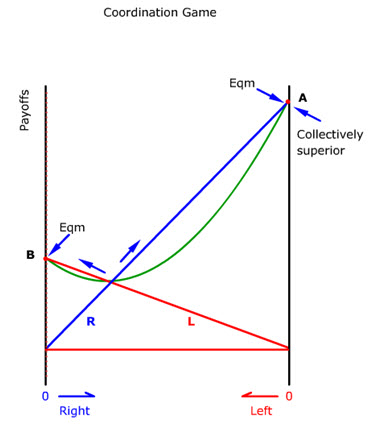
A more interesting strategic game happens when the dominance of payoffs reverses itself somewhere along the horizontal axis.
(Show both payoff curves) Here the R dominates L past the intersection point as more people choose R; and L dominates R past the intersection point as more people choose L. In other words, people prefer to be with the majority regardless of what the option might be. So the payoff for R goes up when more people are choosing R (animate). And the payoff for L also goes up as more people are choosing L (animate).
Letís generate the collective payoff curve by computing the weighted average of the two payoffs (animate). (animate) Here we have two equilibrium solutions. Everybody choosing R is stable on the right at A and everybody choosing L is stable on the left at B.
If the top payoff on the right is the same as the top payoff on the left, people should be indifferent between all choosing R at A and all choosing L at B. But if the top payoff on one side is much lower than the other side, choosing the wrong side might get everybody trapped in a stable but collectively inferior equilibrium (animate).
For example, having a unified measurement system is definitely better than having many competing systems. But one unified measurement system may be superior to other measurement systems. The choice between the American and the metric systems of measurement comes to mind.
The Congestion Game
Due to congestion, the payoff declines for R as more people are choosing R (animate). The same for L (animate). Simultaneously, the payoff for L increases as more people choose R due to relief of congestion on L and vice versa (show both curves). The strategic behavior is to do the opposite of what most other people do.
When the payoff curves for R and L are symmetrical, the collective payoff curve shows that the collectively superior and stable solution occurs at the interaction (animate). But if the payoff curves are not symmetrical, the collectively optimal solution is somewhere to the right or left of the intersecting point of the payoff curves (animate). But uncoordinated pursuit of self-interests will ensure that this optimum is not reached. Instead, the stable equilibrium occurs at the intersection point B.
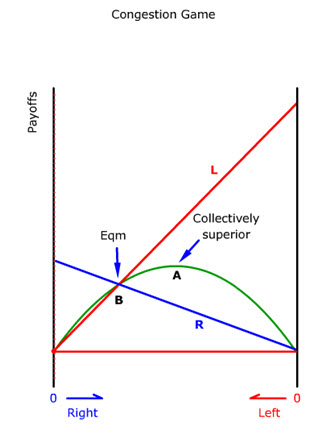
The choice between staying home and going out after a snowstorm is an example of such a congestion game. Those who stay home benefit those driving on the road and vice versa.
The Critical-Mass Game
In some game situations, there could be a double reversal of payoff dominance when the payoff of one option increases at a decreasing rate. Suppose the payoff for R is such a curve (animate blue line). With the payoff for L falling (animate red line), the payoff curve of R intersects the payoff curve of L twice. So L dominates R until a critical mass is reached (circle lower intersection point). After that, the mutual positive externality of choosing R attracts more people for that option. And when most people are choosing R (circle upper intersection point), some individuals might gain by not choosing R.
This double reversal of payoff dominance produces two stable equilibriums (animate). The superior equilibrium occurs near the right end at A and the inferior equilibrium occurs at the extreme left end at B.
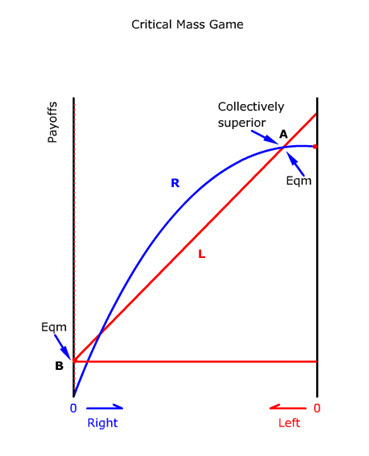
The network effect of many communications systems comes to mind. When few people own fax machines, their usefulness is limited. As more and more people own fax machines, they become very useful and it pays to own one too. But when most people have fax machines, some people can free-ride on those who own the machines.
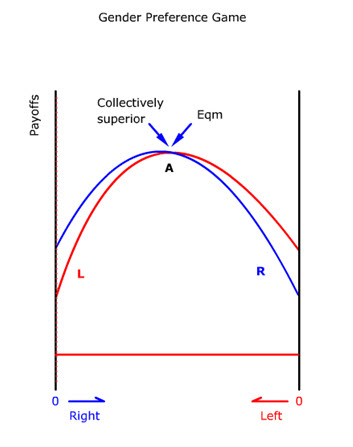
The Gender Preference Game
In the case of birth gender distribution, the objective payoff is higher when the gender ratio is about half and half regardless of oneís preference for boys or girls. Suppose R represents the preference for boys. The payoff curve might look like an inverted U (animate). And the same for the L payoff curve for girls (hide R and animate L). But if there is a universal preference for R (say boys), the payoff for R may dominate the payoff for L (show both curves). If parents can freely choose the gender of their babies, all babies will be boys since having girls is everywhere inferior to having boys. The collective payoff curve shows that an all-boys solution at B is stable (animate). But the all-boys solution, though stable, is inferior to a more mixed gender ratio at A (animate).
But if the preference for boys depends on the scarcity of girls and vice versa (animate), then the payoff curves would reverse their dominance where the gender ratio is about half and half. Here the stable solution at A is also collectively superior (animate).
Summary (Strategic Behavior)
:ē The payoff of oneís action depends on othersí choices.
ē Groups can easily get trapped into stable but collectively inferior solution.
ē A contrarian choice might be a win-win (Pareto superior) move.
ē Be careful about what you wish for.
