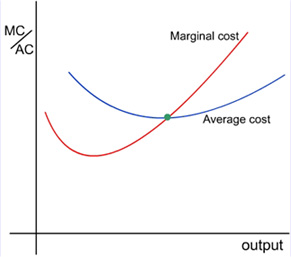
Many students who have seen the following diagram depicting the relationship between marginal cost and average cost have a hard time remembering where the two curves intersect and which curve is above or below the other.
When I was a student, I used to draw the U-shaped average curve first. Then I memorize the following rules of thumb:
• When the average curve is rising, the marginal curve is above the average curve;
• When the average curve is at its minimum (i.e., neither rising or falling), the average value is equal to the marginal value;
• When the average curve is falling, the marginal curve is below the average curve.
These three rules together mean the marginal curve has to intersect the minimum point of the average curve and be below the falling segment of the average curve and above the rising segment of the average curve. Whether the marginal curve that lies below the falling segment of the average curve is rising or falling should not distract our attention.
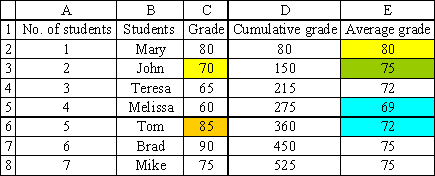
A concrete example might further clarify the situation. Suppose you set up an Excel file to help your instructor compute the average grade of his class. As you add the grade of each student to column C, a new average grade is computed in column E. You will notice that if the additional grade is below the previous average grade (C3 = 70 < E2 = 80), the new average grade will fall (E3 = 75 < E2 = 80). The additional grade (C3) is thus analogous to the marginal value. Conversely, if you see that the new average value rises after a new grade is added (E6 = 72 > E5 = 69), you can infer that the new grade (the marginal value) must be above the previous average value (C6 = 85 > E5 = 69).
So to recap the rules of thumb:
AC ↑, MC > AC
AC ↓, MC < AC
AC ↔, MC = AC