Introduction

Everybody loves free parking. But when the number of parking spaces is fewer than the number of drivers who want to park, free parking may squeeze out those drivers with more urgent needs.

Demand for parking

Suppose the need for parking is reflected by the maximum price (reservation price) one is prepared to pay rather than going without, the demand curve for parking may look like a downward sloping curve. The driver with the most urgent needs is prepared to pay $10 a day (draw circle) and the driver with the least urgent needs will park only if it is free (draw circle). In between, drivers’ demand is arranged by descending order of their needs.

Consumer surplus from free parking

When the number of parking spaces is equal to or more than the number of cars needing parking (animate), free parking results in maximum utility. This utility is measured by the green area under the demand curve (animate). Because the green area represents utility that is not paid for when parking is free, it is called consumer surplus (animate).

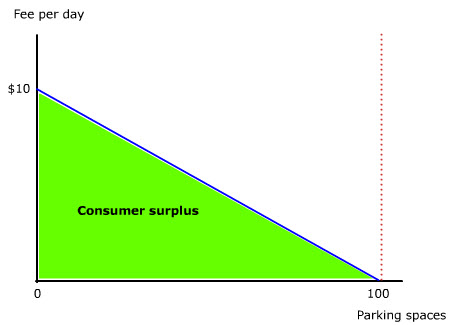
When the number of parking spaces is fewer than the number of drivers needing parking, this consumer surplus is reduced by the uncertainty of not finding a space. Specifically, when the number of spaces is reduced by 50% (animate), the utility of a space is also discounted by 50% if parking is kept free of charge. (animate). The reduced green area thus represents the probabilistic consumer surplus.

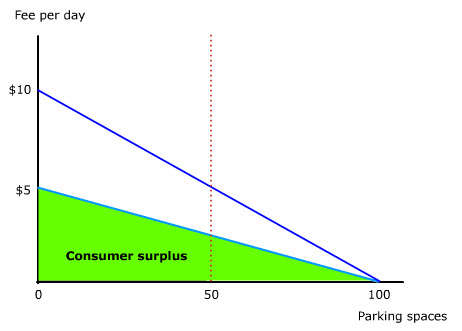
Not only is consumer surplus reduced, its distribution may also be insensitive to the differing needs of drivers. Drivers with less urgent needs may end up occupying spaces that drivers with more urgent needs are prepared to pay for. The time they spend looking vainly for spaces is a deadweight loss to the economy.

Paid parking

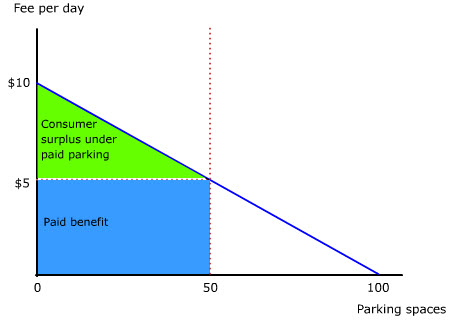
Suppose a fee of $5 per day is charged for parking (animate). At this level, the number of spaces demanded is exactly equal to the spaces available. The market clears because nobody who is prepared to pay $5 is denied a space. They no longer have to waste time hunting for spaces. And those who are not prepared to pay $5 simply look for alternatives.

The total benefit of paid parking consists of the blue area (animate) and the green area (animate). The blue area represents the paid benefit received by drivers. It is also the total revenue received by the parking lot owner (animate). The green area represents unpaid benefit that drivers with more urgent needs would have been prepared to pay if not for the uniform parking fee. In other words, it is the consumer surplus under paid parking (animate).

Comparison

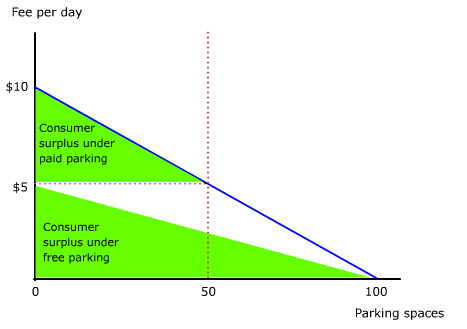
Let us compare the benefit of paid parking vs free parking (animate forward). If the total benefit of paid parking (animate back) exceeds the probabilistic consumer surplus under free parking (animate forward), then paid parking (animate back) is more efficient than free parking (animate forward).

We only need to compare the blue area with the large green area (animate). It turns out that the large green area is equal in area to the blue area (animate). So the total benefit under paid parking exceeds the total benefit under free parking by the consumer surplus under paid parking (the checked green triangle).

Sure enough, consumer surplus under free parking exceeds consumer surplus under paid parking (animate). But it is total benefit that counts (animate).

Summary

To summarize, when parking spaces are scarce, free parking is inefficient (animate). The time spent on hunting for free spaces is wasted. And drivers with more urgent needs may be squeezed out by drivers with less urgent needs. Consumer surplus under paid parking is smaller than consumer surplus under free parking. But it is total benefit that counts. And total benefit of paid parking always exceeds the total benefit of free parking when parking spaces are scarce (animate).