Gaining through Comparative Advantage - recording transcript
Combined PPC
Suppose we have a simple economy with 2 self-sufficient producers Jane and Tom producing only grapes and nuts.
Here is a table showing how much time each producer takes to produce one unit of grapes or nuts.
It shows that Tom takes less time to produce both goods than Jane. We can say Tom has an absolute advantage in producing both goods.
It seems that Tom would not benefit from pooling resources with Jane. But let's convert these time per unit output numbers into output per unit time numbers by taking the reciprocal of each table cell.
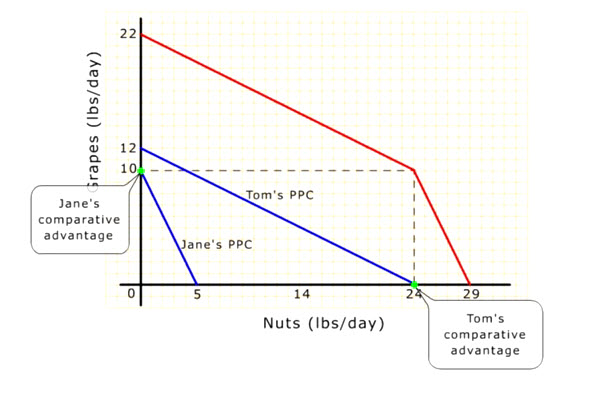
Now we can plot these numbers into production functions for Tom and Jane. Jane can produce a maximum of 10 lbs. of grapes or 5 lbs. of nuts per day. Her linear production function is a straight line connecting the vertical and horizontal intercepts. This function shows the various combination of grapes and nuts that Jane can produce in a day.
This production function is commonly known as the production possibilities curve (PPC for short) or production possibilities frontier (PPF for short)
We can plot Tom's production function similarly.
Tom's production function is everywhere above Jane's indicating that Tom has an absolute advantage over Jane in the production of both goods.
But the relative slopes of the functions are different indicating that the relative costs of production are different between Tom and Jane.
Specifically, Jane gives up fewer nuts than Tom to produce each unit of grapes. In other words, Jane has a lower opportunity cost in producing grapes. Lower opportunity cost means comparative advantage. So Jane has a comparative advantage in producing grapes.
Similarly, we can show that Tom gives up fewer grapes to produce each unit of nuts. So Tom has a comparative advantage in producing nuts.
Jane's comparative advantage in producing grapes thus opens the door to greater total output of grapes and nuts by pooling resources with Tom.
To demonstrate this outcome, let's first generate a combined production function.
The vertical intercept of the combined production function is the sum of the maximum grapes output from Tom and Jane when both are producing grapes exclusively.
The horizontal intercept of the combined production function is the sum of the maximum nuts output from Tom and Jane when both are producing nuts exclusively.
Starting from the vertical intercept, A, where only grapes are produced. If we want to have some nuts, the producer that has the comparative advantage in producing nuts, Tom, should be the one to do so. So the combined production function should move along Tom's production function until Tom completely specializes in the production of nuts at point C.
If we want to produce even more nuts, then Jane (the higher-cost nut producer) should start producing nuts.
The combined production function shows that the relative slope is getting steeper beyond point C because we are moving from the lower-cost to the higher-cost nut producer.
Autonomy vs specialization
All points along the combined PPC represent the combined output of Tom & Jane with at least one of them specializing according to their comparative advantage.
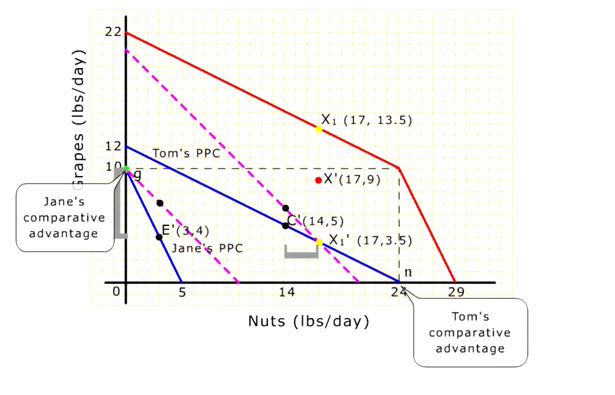
Let's move down the combined PPC from the vertical intercept and observe where the producers are on their respective production functions corresponding to each point on the combined PPC.
If Tom (C') & Jane (E') are each producing for his/her own consumption...,
... their combined output (X') is below their combined PPC.
Both X1 & X2 are feasible & better than X' if at least one of them specializes.
Comparing X' (which is below the combined PPC) with X1 (which is on the combined PPC), for example, X1 has the same amount of nuts but 4.5 lbs. more grapes than at X'.
To get to X1 on the combined PPC from X', Jane must completely specialize in grapes, and Tom must produce a little more nuts.
Jane will have more grapes than she wants, and Tom will have more nuts than he wants. But if they can trade their surplus nuts and grapes at a mutually beneficial rate (such as the pink dotted line), Tom and Jane will end up better off than their positions under autonomy.
Foreign trade
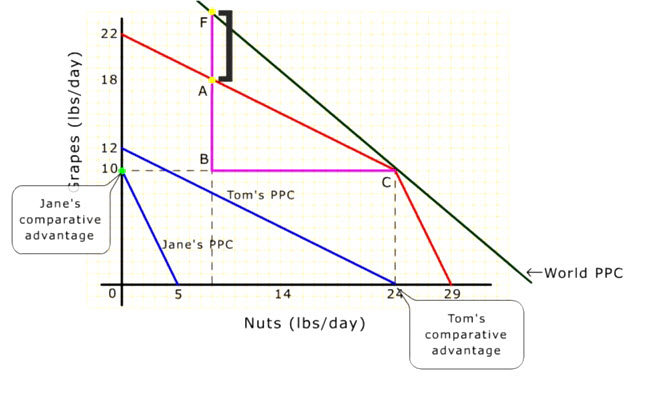
Without foreign trade, the combined PPC represents the best possible combined output of grapes and nuts from Tom & Jane with at least one of them specializing according to their comparative advantages.
If they decide to produce at point "A", only Jane is specializing according to her comparative advantage.
But, if Tom & Jane trade with the outside world along the World PPC that has a more favorable trading ratio between grapes & nuts, ...
... then both Tom & Jane can completely specialize by moving from point "A" to point "C".
At point "C", both Tom & Jane completely specialize.
If Tom & Jane move from point "C" to point "E" by trading nuts for grapes, ...
... they are better off than at point "A," with more nuts & the same amount of grapes.
If Tom & Jane move from point "C" to point "F" by trading even more nuts for grapes, ...
... they are better off than at point "A," with more grapes & the same amount of nuts.
Conclusion
Therefore, partial or complete specialization according to comparative advantage is a win-win strategy to increase total output, even though one party might enjoy absolute advantage over another party.